Suppose there are two types of investors in the Three-Firm Case, both with quadratic utility functions. In topic 7.4, Investor Risk Preferences you saw that if investor preferences are defined over wealth, then an equivalent set of preferences, defined over returns, can be derived.

We carry out this construction for the Three-Firm Case. Let the two types, I and II, have quadratic preferences defined over wealth:

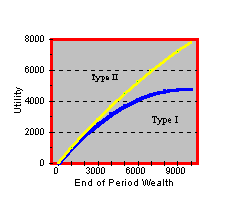
Note that the greater the curvature away from a straight line, the more risk-averse an individual is. In the Figure 7.4, observe that Type II is less risk-averse than Type I.

Now let us consider an investor's indifference map defined over risk and return. In the topic Investor Risk-Preferences, we showed that this requires a simple transform of the coefficient of risk-aversion, c. The re-scaling required is:

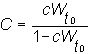
As a result, the general form for quadratic preferences defined over returns is:

From the definition of C, you can see that C is simply c (the coefficient of risk-aversion) re-scaled to adjust for initial wealth.

If initial wealth is $2,688 then for Type I, C equals:

Therefore, Type I's preferences over returns are given by:

The relationship depicted in Figure 7.4 remains the same.

An implication of risk-averse investors is that there must be a positive risk-return tradeoff in the capital market. We discuss this next, in the topic Market Price of Risk.

(C) Copyright 1999, OS Financial Trading System