7

7.6 MARKET PRICE OF RISK

Risk-aversion imposes restrictions on the Capital Market Line. Investors who are risk-averse demand compensation for assuming risk. They differ from gamblers, who are willing to pay a premium to assume risk!

In the capital market, risk-aversion results in a capital market line (CML) that has a positive slope, as illustrated in Figure 7.5.

Figure 7.5

The Capital Market Line in a Risk-Averse Market

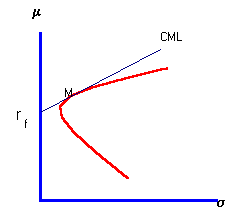
Recall that the slope of the CML is called the market price of risk. In the theory, both rf and the market price of risk determine the point of tangency, M, between the minimum-variance frontier for risky securities and the capital market line.

You can verify the next few statements using CAPM Tutor's default data file in the subject titled CAPM. As you vary the risk-free rate, different points of tangency are attained. However, if you choose an rf that is too high, then no point of tangency will exist!

If there is no tangency point, we cannot be at a capital market equilibrium. This is because all investors prefer to hold the risk-free asset, and hence demand dries up for the risky securities. In this case, however, you would expect prices to adjust. In particular, returns from holding risk securities will have to become more attractive. This in turn will change the shape of the minimum-variance frontier. The end result of this adjustment process is that in a capital market equilibrium, the price of every risky asset is determined and a point of tangency exists. In topic 7.12, Equilibrium Value of the Firm you will study this issue formally.

You can observe these dynamics by varying the risk-free interest rate in CAPM Tutor. You should click on the subject "Market Equilibrium" and then click on Calculate. This will display the now familiar CML and minimum-variance frontier for the default risk-free rate of 12% in the Three-Firm Case. The matrix displays the equilibrium prices and other key statistics.

You can see what happens when the risk-free rate is increased to some higher rate. Observe that the equilibrium prices adjust as do returns, betas etc. Similarly you can look at what happens to the capital market equilibrium when the risk-free rate of interest falls. You may want to think about whether the predicted adjustment corresponds to actual market behavior.

Capital market equilibrium with risk-averse investors requires the expected return at point M to be greater than the risk-free interest rate. This means that the CML has a positive slope. In Figure 7.5, E(rM) is the expected return and sM is the standard deviation at point M. The slope of the CML is

Suppose you are an investor in this market. This slope tells you how much return you must give up to achieve a reduction in risk. That is, for the market as a whole, this slope measures the market price of risk.

In the Three-Firm Case, the market price of risk is determined by the expected return on the market portfolio (0.159), the risk-free rate of return (0.12), and the standard deviation of the market portfolio (0.113). As a result, the market price of risk in the Three-Firm Case is:

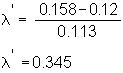
To see how the market price of risk results from a population of risk-averse investors and how prices are determined click on the topic The CAPM in Equilibrium.

previous topic

next topic