![]() 6.10 THREE-FIRM CASE: DERIVATION OF THE SML
6.10 THREE-FIRM CASE: DERIVATION OF THE SML
Let M be the portfolio that forms the point of tangency between the capital market line and the efficient frontier for risky securities. Recall that this is the portfolio that maximizes the slope of the capital market line. For the Three-Firm Case these values are as shown in Table 6.5.
|
Table 6.5 |
|
|
Tangency Portfolio |
|
|
Portfolio M |
|
|
Expected Return |
0.159 |
|
Firm 1 weight |
0.530 |
|
Firm 2 weight |
0.155 |
|
Firm 3 weight |
0.315 |
|
Standard Deviation |
0.337 |
|
Slope |
0.116 |
As a first step in the Three-Firm Case, we need to characterize the variance-covariance of returns for each firm with the market portfolio M. The population distribution for the three-firm problem generated from the set of possible states of the economy appear in Table 6.6.
|
Table 6.6 |
|
Distribution of Returns |
|
State |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Expected Return |
Standard Deviation |
|
Firm. 1 |
0.821 |
0.821 |
0.821 |
0.143 |
0.107 |
0.071 |
0.143 |
1.429 |
1.679 |
1.679 |
0.229 |
0.961 |
|
Firm 2 |
0.846 |
0.808 |
0.615 |
0.192 |
1.538 |
1.500 |
1.500 |
0.231 |
0.231 |
0.231 |
0.138 |
0.928 |
|
Firm 3 |
1.200 |
1.200 |
0.960 |
0.120 |
0.120 |
0.200 |
0.600 |
0.600 |
0.600 |
0.600 |
0.052 |
0.727 |
|
Market Portfolio |
0.189 |
0.183 |
0.228 |
0.143 |
0.144 |
0.207 |
0.119 |
0.533 |
0.665 |
0.665 |
0.159 |
0.337 |
From the population distribution, you can calculate the covariance of each security with the returns from portfolio M and also the betas of the securities. See Table 6.7.
|
Table 6.7 |
|
Returns, Covariances and Betas |
|
Portfolio |
Expected Return |
Covariance with M |
Beta |
|
Riskless |
.12 |
0 |
0 |
|
Firm 1 |
0.229 |
0.316 |
2.78 |
|
Firm 2 |
0.138 |
0.054 |
0.47 |
|
Firm 3 |
0.052 |
-0.198 |
-1.74 |
|
Market Portfolio |
0.159 |
0.113 |
1 |
In the last row of Table 6.7, the covariance of the market portfolio with itself is the total variance of the market portfolio, and therefore the square-root of this term is the total risk. That is, the total risk of the market portfolio M is 0.3369. In the fourth column of table 6.7 we present each security's beta.
Recall that the definition of beta is:
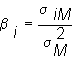
where the numerator is the covariance of security i with portfolio M, and the denominator is the total return variance of the portfolio M. By substituting the numbers from table 6.7, you can verify the fourth column.
Now, recall that the SML implied from the market portfolio M is:
![]()
where the beta of security i is provided above. Thus, substituting our estimates for beta into the SML gives us the expected return from each firm:
![]()
![]()
![]()
The expected returns implied by the efficient set mathematics result in the same expected returns as computed from the return distribution.
previous topic
next topic
(C) Copyright 1999, OS Financial Trading System