chp77.9

7.9 TWO-FUND THEOREM

Figure 7.7 (reproduced here) combines both investor behavior and the investment opportunity set. Recall that the CML line (shown in green on-line) represents the set of undominated portfolios in a capital market where investors can borrow and lend at the risk-free interest rate. The blue line represents the minimum-variance frontier constructed from all risky assets. Finally, the red and pink lines represent indifference maps for investors with different degrees of risk-aversion.

Figure 7.7

Two Risk-Averse Investors

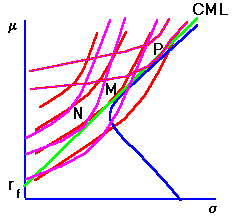
As we have seen, an expected utility maximizing investor will select a portfolio at the point of tangency between the CML line and their indifference curve. Such a point is always a combination of the market portfolio, M, and the risk-free asset. For example, in this graph, portfolio N is long on both the risk-free asset and M, whereas portfolio P is short on the risk-free asset and long on M.

This allows us to formally state the two-fund theorem:

If investors care only about the expected return and the standard deviation of their portfolio return, then every investor holds a portfolio consisting of M and the risk-free asset.
Implications of the Two-fund Theorem

1. Interpretation of Portfolio M

Before developing implications of this theorem, we need to introduce some notation. As described above, any portfolio on the CML is a combination of the risk-free asset and the market portfolio. We represent this by a number ak, where ak is the fraction of wealth in the risk-free asset, (1- ak) is the fraction of wealth in the market portfolio, and k refers to the kth investor.

If ak = 1, the investor only holds the risk-free asset. If ak < 0, the investor is short the risk-free asset and long M, and if ak > 0 but less than 1 the investor is long both the risk-free asset and M.

Let W be the total wealth of investor k, and Yk = (1- ak)Wk the amount of wealth invested in the market portfolio.

Finally, portfolio M consists of different individual securities. Let mi = firm i's weight in M. You can think of mi as follows. In order to obtain expected return E(rM ) and standard deviation sM, you must invest fraction mi of your wealth in security i.

Let us now consider what the mi implications are for market equilibrium.

In equilibrium, demand equals supply. Therefore, the total wealth invested in M must equal the total market value of M. In other words, if we ask each investor how much money they have invested in M and add this up, we get the total wealth invested in M.

Similarly, if we look at the prices of all securities in the market, multiply them by the number of shares of each asset, and add up these numbers, we get the market value of M. Clearly these must be equal. Further, we can do this asset by asset, and the market value of a asset must equal the amount invested in it by all investors.

The total market value of shares in risky firm i is Vi = Pi Qi, where Pi is the share price of firm i and Qi is the number of shares issued by firm i. Vi is also called the market value of firm i.

Let Yk be the money invested in the market portfolio M by investor k. Then, in our notation, miYk is the amount invested by investor k in firm i. Equality between the total market value and the sum of amounts invested in firm i by each investor, implies that

Solving for mi, we get: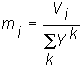

That is, the share in the market portfolio equals the value of firm i relative to the total wealth invested in all risky securities.

But we also know that

because the total amount invested in the market must equal the market value of these securities. Substituting, we get:

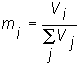
which says that the share of asset i in M is simply equal to the market share of asset i. This is why M is called the market portfolio.

2. The Individual Investment Decision

Another interesting implication of the two-fund theorem is that the proportion an investor holds in every firm is constant. To see why the proportions remain constant, consider the following.

Let Vi and Vj denote the values of firms i and j, and let z(i) and z(j) be the proportions of the firm values i and j held by investor k, so that the dollar amount spent on firm i is z(i)Vi by investor k. To simplify notation, we have written the proportion as z(i) instead of as zk(i).

Our objective is to demonstrate that the two-fund theorem implies that the proportion of each firm held is the same for any investor, i.e. z(i) = z(j). Of course, the magnitudes of these proportions depend upon an investor's personal wealth.

Recall, that Yk is the dollar value of k's wealth invested in risky securities, and mi was the share of firm i in the market portfolio. The dollar value of firm i in k's portfolio is miYk. This is the proportion of investor k's total wealth invested in risky securities, that is invested in firm i.

Since the dollar amount spent on firm i by investor k is the same as the proportion of k's wealth invested in the risky asset i we get z(i)Vi = miYk. The proportion of each firm held is equal, i.e.,

Since

where V is the total value of all firms, rearranging leads to

Therefore z(i) = z(j), and this implies that

This result should not be confused with naive diversification. In that case an equal amount of wealth was allocated to each asset in a portfolio. The implication here is very different.

To summarize, the implication is that each investor holds a constant share of the entire market portfolio of risky securities, and that they hold a constant share of each firm in the market. This result would coincide with naive diversification only if every firm happened to have the same total market value.

A final implication from expected utility maximization and the two-fund theorem is that irrespective of how risk-averse an individual investor is, if the expected return on the market portfolio M is strictly greater than the risk-free rate of return, then every expected utility maximizing investor will hold some positive proportion of the risky market portfolio M.

This is shown in the topic Risk-Aversion and the Market Portfolio.

previous topic

next topic