![]() 7.14 FIRM VALUE: A GENERAL EQUILIBRIUM CONSTRUCTION
7.14 FIRM VALUE: A GENERAL EQUILIBRIUM CONSTRUCTION
Formal construction of the equilibrium value of the firm uses some advanced microeconomic theory.
Notation
Firms are indexed by the letters i and j, while investors are indexed by the letter k. Each firm has cash flow that depends on the state of the economy. A state is a complete description of all exogenous factors. For example, the state summarizes labor costs, raw material costs, the weather, and any other factor that affects the cash flows of a firm. We index states by the letter s. We use the following notation.
x
j(s)p
(s)m
js
ijr ![]() One plus risk-free rate (borrowing and lending take place at this interest rate.)
One plus risk-free rate (borrowing and lending take place at this interest rate.)
F ![]() Final level of wealth
Final level of wealth
![]()
![]() Proportion of firm j demanded by investor k.
Proportion of firm j demanded by investor k.
W
kU
kV
jWe construct a competitive capital market equilibrium such that:
1. All investors choose portfolios to maximize their expected utility subject to wealth constraints.
and
2. All risky asset markets clear.
The starting point for constructing a capital market equilibrium is to define the end-of-period wealth for some investor k contingent upon the state of the economy, s. This will permit construction of each investor's expected utility maximizing demand for each risky security.
Demand for Each Firm
Denote the end-of-period wealth for investor k contingent upon state s being realized by Fk(s). For any portfolio of risky and risk-free assets, this can be partitioned into the 1 plus risk-free return earned on total initial wealth plus excess return over the risk-free return.
![]() (7-1)
(7-1)
In this expression, rWk is the return from initial wealth, and the second term is the sum of excess firm returns weighted by the proportion invested in each firm.
The expected utility of final wealth for type i is:
![]() (7-2)
(7-2)
With no restrictions on short selling, the first order condition for expected utility maximization with respect to proportion of each firm demanded (z) is:
![]() (7-3)
(7-3)
where E denotes the expectation of the expression in brackets. The simplifying statistical relationships that Mossin uses are:
![]() (7-4)
(7-4)
![]() (7-5)
(7-5)
![]() (7-6)
(7-6)
![]()
as follows:
![]() (7-7)
(7-7)
Observe that the preference type enters the demand equation in a multiplicative way. Therefore we can solve for an intermediate
zj that when multiplied by a factor for investor k provides the required demand![]()
This form of preference separation result is the economic underpinning of the two-fund theorem. As a result, let the solution to the following problem
![]() (7-8)
(7-8)
be denoted as:
![]()
Then, equation
![]() (7-9)
(7-9)
provides
![]()
In equilibrium, it must be the case that
![]()
i.e. the sum of the proportions held by the different investors must equal one. This yields:
![]() (7-10)
(7-10)
and rearranging (7-10) we get
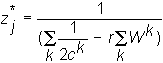 (7-11)
(7-11)
From (7-9) and (7-11) it follows that
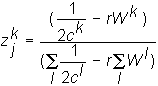 (7-12)
(7-12)
Observe from (7-12) that investor k's demand for firm j is independent of firm j itself, which is the separation result. Let zk be the proportion of every firm demanded by investor k.
Using this result, it becomes relatively simple to solve for Vj, which is the market value of firm j. The demand equation, (7-7) can now be written as
![]() (7-13)
(7-13)
Since
![]()
we get
![]() (7-14)
(7-14)
Next, we use the fact that
![]()
which says that the market value of all assets must equal the total wealth in the economy. Substituting this into (7-14) and re-arranging, we get
![]() (7-15)
(7-15)
Finally, rearranging (7-15), we can solve for V :
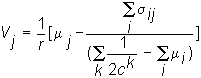 (7-16)
(7-16)
Equation (7-16) is a valuation model for the firm as a whole. The equation states that the value of firm j is equal to the present value (at the risk-free rate) of risk-adjusted expected cash flows. The risk adjustment depends upon average investor risk preferences and the covariance of cash flows with all other firms in the economy (i.e., the firm's systematic risk).
We now apply this model to the Three-Firm Case.
previous topic
next topic
(C) Copyright 1999, OS Financial Trading System