![]() 7.13 FIRM VALUE: A GENERAL EQUILIBRIUM DESCRIPTION
7.13 FIRM VALUE: A GENERAL EQUILIBRIUM DESCRIPTION
The CAPM is a very general valuation model for risky securities. In the form that has been developed so far, inputs to the pricing model are the risk and return of the market portfolio, the risk-free rate of return, and the covariance of the individual asset's return with the market portfolio.
A general equilibrium form of the CAPM was first derived by Mossin (1967). The valuation model for the firm (or project) as a whole is derived as the present value of expected cash flows. This also shows you the precise relationships that must hold between investor preferences, the market price of risk, and the value of the firm.
Investors are assumed to be risk-averse and care about their wealth at the end of the period. Specifically, these risk-averse preferences are assumed to have quadratic preferences over wealth.
Each investor chooses some portfolio of risky and risk-free securities to maximize expected utility, subject to initial wealth constraints, given the available supply of financial securities. In a competitive capital market, the price of each financial security adjusts so that securities supplied equal securities demanded.
That is, given a set of prices and some endowment of cash and stocks, each investor computes their individual demand for each risky security. This demand may be positive, in which case shares are purchased. Or the demand may be negative, in which case shares are sold.
For example, if an individual's current holding in Firm 1 is 300 shares, and their demand is 250, then the excess demand is -50 shares. Therefore this investor will sell 50 shares in Firm 1 at the prevailing price. The excess demands can be computed for every investor in the market and summed over for the market as a whole. Markets clear when this sum is zero.
Consider what happens if markets do not clear. If an excess positive demand occurs in any stock market, then it is reasonable to assume that the stock price will be bid up by investors. Similarly, if an excess negative demand occurs then price will fall. At each new price, excess demands are reevaluated, until in equilibrium the excess demand in each stock market is zero. The set of prices that attains this equilibrium state is referred to as the set of market clearing prices.
We later construct each firm's value in equilibrium. Critical to this construction is the role played by quadratic preferences, which imply that only the first two moments of the return distribution (the mean and the variance) are relevant to any investor. (An equivalent assumption for attaining the same result is the assumption of normally distributed returns.)
Once again, the two-fund theorem plays an important role in this general equilibrium analysis. The value of the firm that results is:
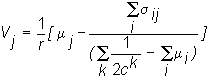
This form of the CAPM evaluates total cash flows from the firm. Here,
mj is the expected total cash flow from firm j, and sij is the covariance of cash flows between firms i and j. In this form of the CAPM, we have written the discount rate, r, as 1 plus risk-free rate. The equation states that the value of firm j is equal to the present value (at the risk-free rate) of risk-adjusted expected total cash flows. The first term in the brackets is the cash flow; the second term is the risk-adjustment.The risk adjustment depends upon two terms. The first term in the denominator is the average of investor risk preferences. The term ck is the coefficient of risk-aversion for Investor k, discussed in topic 7.4, Investor Risk Preferences. The numerator of the risk adjustment term is the sum of the covariance of cash flows with all other firms in the economy. That is, only the firm's systematic risk matters.
The equation tells you the total value of a firm as a function of expected cash flows, the covariance of cash flows, and investor risk-preferences. To obtain the stock price, simply divide by the number of shares.
We now turn to the formal construction of the equilibrium firm value of the firm's valuation equation, followed by an application to the Three-Firm Case.
previous topic
next topic
(C) Copyright 1999, OS Financial Trading System