6

6.3 DERIVATION WITHOUT SHORT SALES

Formally, the no short sales problem resembles Markowitz diversification with additional constraints that restrict all portfolio weights to be non-negative:

subject to

for all i = 1,.......,N.

The first constraint fixes the desired expected rate of return, and the second constrains the portfolio weights to sum to one. The final set of N constraints places the no short selling restriction on the portfolio weights. As with short selling, the solution to this problem satisfies dominance because it minimizes variance subject to a fixed expected return constraint.

The solution to this minimization problem is the same as the solution to the problem with short selling whenever the no short sales constraint is not binding. In general, however, some of the set of inequality constraints will be binding, and the previous solution will not solve this problem.

Observe, however, that while the objective function (portfolio variance) is non-linear, all the constraints are linear. Therefore the feasible set is convex. As a result, a set of conditions known as the Kuhn-Tucker conditions can be applied to find the optimal portfolio.

Again we can use the Lagrange form of the risk minimization problem, where the portfolio weights (i.e., alphas) are choice variables and the lambdas are Lagrange multipliers:

The Kuhn-Tucker necessary conditions are:

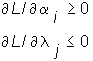
and finally,

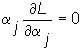
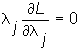
i = 1, .. ,N, j = 1,2

Let the expected return and the sum of the portfolio weight constraints be denoted as g1 and g2 . If the solution satisfies these constraints at equality (i.e., the target expected return is exactly met and all cash is invested), then for our problem, the Kuhn-Tucker conditions are valid. However, the solution must satisfy the constraint qualification

for the jth constraint where the subscript notation for g refers to the partial derivative with respect to the a, (having the same subscript), evaluated at the solution. These are always satisfied in our case. Finally, the second-order conditions are met as in the case with short selling.

The Kuhn-Tucker conditions characterize a solution but do not readily provide a way to compute the solution. Various numerical methods have been developed to solve such problems, which generally go under the name of "quadratic programming."

previous topic

next topic