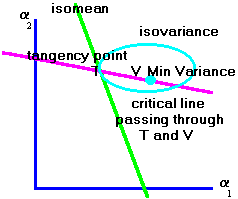
Because the critical line is a straight line, it can be constructed from two points. We have seen how to construct the minimum-variance portfolio and we can solve for any single point of tangency between the Isovariance and Isomean graphs by equating the slopes at the tangency point. The critical line shown in Figure 5.8 satisfies the equation of the straight line that passes through these two points.

Using CAPM Tutor, you can construct this critical line graphically by repeatedly clicking on different points along the minimum-variance frontier in the Geometric Derivation subject.

In Chapter 6, the Capital Asset Pricing Model, we extend the theory of mean-variance efficient portfolios to the problem of pricing risky securities.

(C) Copyright 1999, OS Financial Trading System