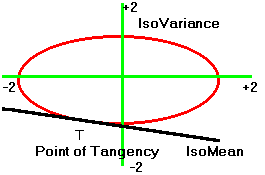
The final building block required to construct the critical line, is one point of tangency between the isomean/isovariance graphs. You can first see this tangency point graphically, using CAPM Tutor, and then read how it is constructed in this topic.
Using CAPM Tutor, click on the Frontier button and then choose any point along the minimum-variance frontier by clicking. This fixes a portfolio, and so a target return and portfolio variance is displayed numerically in the data entry window. The point of tangency will be displayed in a similar manner as in Figure 5.5.
|
Figure 5.5 |
|
Portfolio Weights |

To construct this point of tangency we proceed by considering each element of Figure 5.5. First, consider the family of isovariance ellipses.
|
Figure 5.6 |
|
Isovariance Ellipses |
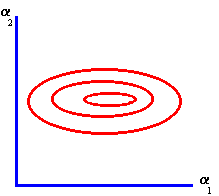
Recall that the general form of the isovariance ellipse is
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Viewing
a2 as an implicit function of a1, we can differentiate the equation of the ellipse implicitly with respect to a1 to find the slope:![]()
where the derivative of
a2 with respect to a1 is defined as:![]()
Collecting terms yields:
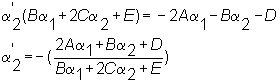
Equating this slope to that of the isomean line lets you solve for the point of tangency. Recall that the equation of the isomean line is :
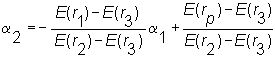
So the slope of the isomean line equals
![]()
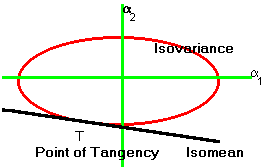
which is illustrated in Figure 5.7.
|
Figure 5.7 |
|
Isomean/Isovariance Graphs |
The last part of this chapter deals with the construction of the critical line.
previous topic
next topic
(C) Copyright 1999, OS Financial Trading System