5

5.3 ISOVARIANCE ELLIPSE

Similar to the idea of an isomean line is the idea of an isovariance ellipse. Here, we choose portfolio weights to provide some target level of risk. Then the standard deviation of returns from a three-firm portfolio is a quadratic equation in portfolio weights. You will see that choosing weights to give a constant target risk results in an ellipse in portfolio weight space.

The objective here is to construct the set of portfolio weights that provide the same portfolio standard deviation for the general three-firm problem, and then to verify that this is indeed an ellipse. To make life simpler, let us work initially with the square of the risk, which is the portfolio variance. First, the portfolio variance equation is:

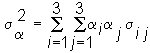
Again substituting a3 for 1 - a1 - a2, yields an equation of portfolio weights having a quadratic form.

This quadratic form can be rearranged into the general form for an equation of second degree in a1 and a2.

The general form for an equation of second degree is:

Rearranging the portfolio variance equation yields the general form if we let

For our Three-Firm Case, these values are:

By applying the graphical properties of second degree equations if the sign of the discriminant, (B2 - 4AC), is negative, then the relationships among the portfolio weights form an ellipse. The ellipse collapses down to a single point when the target variance is the minimum possible variance.

For the Three-Firm Case, this condition is satisfied:

These ellipses are depicted graphically in Figure 5.3.

Figure 5.3

Isovariance Ellipses

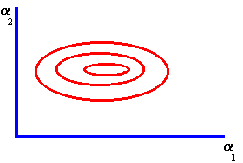
In CAPM Tutor, clicking on different parts of the minimum-variance frontier chooses portfolios with different variances. As a result, by first clicking on the Frontier button and then clicking on different parts of this frontier, you can construct graphically the isovariance ellipse in units of portfolio weights.

The next part of this chapter deals with characterizing the isomean-isovariance tangency points.

previous topic

next topic