A mathematical puzzle, known as the St. Petersburg Paradox, did much to stimulate our understanding of attitudes toward risk. This puzzle involves an investment opportunity whose expected value is infinite.

The question posed is: What are you willing to pay for this opportunity? This payment would surely not exceed a small finite amount. The paradox is to explain the discrepancy between what you would pay and the fact that the expected value is infinite.

One of the first attempts to explain this paradox was by the mathematician, Daniel Bernoulli, who introduced subjective "utility" values of money and computed expected utilities. Much later, this idea was formalized by von Neumann and Morgenstern into a set of rational choice axioms (see Appendix A: Expected Utility Theorem).

This axiomatic work not only formalizes the earlier solutions to the St. Petersburg Paradox but, more generally, it also provides an important means of determining individual attitudes toward risk. The axioms imply that risk attitudes can be summarized by means of a "utility function." This function can be used to guide investment decisions.

Why do we care about rational choice in the theory of investments? The answer is it ensures that no other investor can take advantage of your investment decisions Formally, it means that equilibrium prices are arbitrage-free. Recall that if there is arbitrage, then you can obtain an infinite return without incurring any risk.

Let us give an example of a simple arbitrage opportunity created by a violation of the rational choice axioms. Suppose an investor strictly prefers investment opportunity A to B, and strictly prefers investment opportunity B to C. Rational choice requires that this investor will never make a decision that implies that opportunity C is preferred to A; otherwise there would be an arbitrage opportunity. The arbitrage would arise by round-trip trading with the investor: sell them A, then C for a little more, then B for a little more, then A, and so on.

Operationally, the expected utility theorem implies that investment opportunities can be ranked in terms of expected utility as opposed to expected values. An immediate implication of this representation, applied to outcomes defined in money, is that associated with each risky investment opportunity is a number, referred to as a certainty equivalent or a "price."

This certainty equivalent is defined as the cash amount that makes an investor indifferent between this cash amount and the investment opportunity itself. If an investor is indifferent between the risky opportunity and its expected value, the investor is said to be risk-neutral. If an investor's certainty equivalent is strictly less than the expected value, then the investor is risk-averse. Otherwise, the investor is described as risk-loving.

An example consistent with risk-loving behavior is the observation that individuals are prepared to enter into actuarial "unfair games of chance" at casinos. For example, betting one chip on either red or black on a roulette wheel in France provides the player with an 18/37 chance (and in the US an 18/38 chance), of winning one additional chip. The true probability is 1/2, but the casino adds either a single zero or a single and double zero depending upon which form of roulette, French or American, is played.

When we construct a theory of capital markets, we assume that investors are risk-averse. In terms of risk and return, this means that the indifference curves look like those in Figure 7.1:

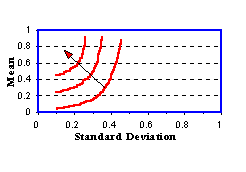
The set of indifference curves in the Figure 7.1 is called an indifference map. Observe that moving in a northwest direction results in both the expected return increasing and risk decreasing. Moving in this direction therefore yields points that provide investors with higher levels of expected utility.

The picture is consistent with the empirical observation that investors must receive a premium for assuming risk. For example, in the debt markets, default-free Government securities have a lower yield to maturity than risky corporate bonds of the same maturity. That is, investors must be compensated for assuming the default risk associated with a corporate bond.

In the next topic we describe The St. Petersburg Paradox, and use this to motivate the concept of expected utility. This is followed by a description of investor preferences over risky assets. An application to the Three-Firm Case is in topic 7.5, an indifference map example.

Finally investor risk preferences allow us to interpret the capital market line in terms of how the market trades return for risk; this is described in topic 7.6, Market Price of Risk.

(C) Copyright 1999, OS Financial Trading System