![]() 7.19 RISK-ADJUSTED DISCOUNT RATES
7.19 RISK-ADJUSTED DISCOUNT RATES
An important reason for deriving an asset pricing model such as the CAPM is to tell us the interest rate to use in discounting risky cash flows. If the market price per unit of risk is estimated empirically, then the return formulation of the CAPM provides the expected return for individual stocks. Equivalently, as demonstrated by the general equilibrium analysis, this is the investor's required rate of return when valuing a risky stream of future cash flows. As a result, this formulation can be applied to value future cash flows in a manner that is more readily related to fundamental and econometric analysis.
Three important variables are estimated in this type of analysis: the magnitude of cash flows, the timing of cash flows, and a discount rate that takes into account the "riskiness" of the cash flows. This "risk-adjusted discount rate" is provided by the "beta" determined in the capital asset pricing model.
The one period expected return from a stock i is:
![]()
where P0 is the current price, P1 is the future price, and D1 is the dividend (if any) to be paid in period 1. The CAPM formula says
![]()
Re-arranging, we get
![]()
so
![]()
The numerator has expected cash flow from the stock, and the denominator equals one plus the investor's required rate of return from the stock. The higher the risk, as measured by beta, the higher the required rate of return and therefore the lower the price for a given set of future cash flows. This is called the risk-adjusted discount rate formulation; we discount future cash flows by an interest rate that has been adjusted for risk.
An alternative approach is to adjust not the interest rate but the expected cash flows from the project. In this approach, the certainty equivalent of the expected cash flows is used to simplify the discounting problem. The problem, of course, is how to adjust the expected cash flows for risk. In the general equilibrium version of the CAPM, the expected cash flows are adjusted by (among other things) the average investor's tolerance for risk. This average cannot be directly observed. It can be inferred from the risk and return behavior of the portfolio of all risky securities.
In terms of observed proxies for this market portfolio the risk-neutral valuation form for risk-adjusted cash flows is derived as follows.
![]()
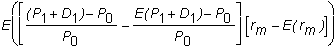
![]()
We can write this as
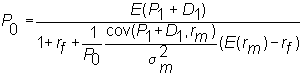
so
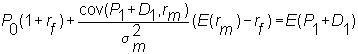
and finally,
![]()
where
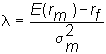
is the market price per unit of risk (relative to the security market line).
In this case, we adjust the numerator to reflect risk and discount at the risk-free rate. The numerator is sometimes called the certainty equivalent of the future cash flows, and this approach is called the certainty equivalent approach.
Both the risk-adjusted discount rate and the certainty equivalent approaches can be applied to the valuation of a firm, or more generally, to any set of future cash flows. We summarize them as follows.
(RADR):
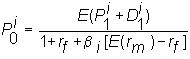
(CEQ):
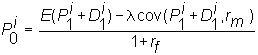
previous topic
next topic
(C) Copyright 1999, OS Financial Trading System