chp44.10

4.10 THE SHAPE OF THE FRONTIER

If you calculate the solution to the risk minimization problem for a large range of expected returns, you generally get a frontier shaped like a "bullet." Some insight into why the frontier curves in the manner shown can be obtained by revisiting the case of two securities with no short selling.

Consider two stocks with expected returns E(r1) and E(r2), standard deviations s1 and s2, and covariance s12. If we take a combination a of the first stock and (1-a) of the second, the expected return from our portfolio Is aE[r1 + (1 - a)E(r2)]. This return lies somewhere on the line between E(r1) and E(r2). The standard deviation of the portfolio Is

In order for the frontier to have the curved shape, then it must be possible for this standard deviation to be less than as1 + (1 - a)s2. That is, there must exist a such that

Squaring both sides and simplifying, this reduces to

Clearly, if , this holds for any a with 0 < a < 1, and does not hold if either a < 0 or a > 1. If s12 > 0, this holds if 0 < a < 1 and

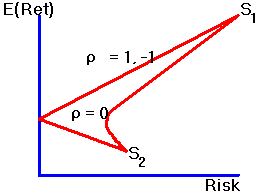
The variable r12 is called the correlation coefficient. It is the value of the correlation coefficient that determines the shape of the frontier. If r12 is less than one, "usual" weights, i.e., 0 < a < 1, will imply that the standard deviation of the portfolio is less than the linear combination of standard deviations. The various frontier shapes, as a function of the correlation coefficient with short selling allowed, are shown in Figure 4.4.

Figure 4.4

Frontier Shape: With Short Selling

It is also easy to see that in the special case where r12 equals either 1 or -1, the frontier will be linear and will touch the Y-axis (i.e., that we will be able to construct a risk-free portfolio). To see this if r12 = -1 (which is true for the example at the very beginning of this chapter), we can construct a zero-variance portfolio as follows:

since

= -1.

= .

This equals zero if

or if

In general, however, it will not be possible to diversify away all risk, and the frontier will have the curved shape shown initially.

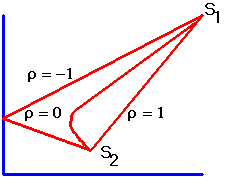
Without short selling, because each security's weight in the portfolio must be non-negative, it is not possible to eliminate all risk unless the two stocks are perfectly negatively correlated, i.e. r12 = -1. The various shapes as a function of the correlation coefficient are shown in Figure 4.5.

Figure 4.5

Frontier Shape: No Short Selling

In Chapter 5, Diversification: A Geometric Approach, for the set of portfolios lying on the efficient frontier, we identify the implied portfolio weight behavior.

previous topic

next topic