![]() 3.3 THREE-FIRM CASE: APPLICATION
3.3 THREE-FIRM CASE: APPLICATION
We can illustrate the concept of naive diversification for three investments in a portfolio. The total variance for a naively diversified portfolio for the Three-Firm Case is given by:
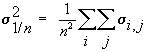
The variance-covariance matrix is in Table 3.1:
Table 3.1
Variance-Covariance Matrix
| State | Expected Return | Variance (i, i) | Covariance (i, j) | Pair (i, j) |
| Firm1 | 0.229 | 0.924 | 0.063 | (1,2) |
| Firm2 | 0.138 | 0.862 | -0.582 | (1,3) |
| Firm3 | 0.052 | 0.528 | -0.359 | (2,3) |
The variance of an equally weighted portfolio therefore equals:
= [0.924 + 0.862 + 0.528]/9 + [2(0.063) - 2(0.582)-2(0.359)]/9
= 0.062
The portfolio standard deviation is:
= 0.249
Observe that the equally weighted portfolio variance for three securities is substantially smaller than the variance of any individual security (0.062 for the portfolio compared to 0.923, 0.862, and 0.528 for the three securities).
The expected return from this equally weighted portfolio is the average of the three expected returns: (0.229 + 0.138 + 0.052)/3 = 0.139. Note that this is approximately the same expected return as that provided by Firm 2 but with a lot less risk. If you were an investor that was faced with the opportunity of :
Firm 2: E(Return) = 0.138, Standard Deviation = 0.371
or an equally weighted portfolio with
E(Return) = 0.139, Standard Deviation = 0.062,
which would you choose? Why?
The answer depends on your preferences toward risk and return. If you agree with the assumptions that we have made to date, the clear winner is the equally weighted portfolio. That is, if investors care only about the expected return and the standard deviation of return, and more expected return is preferable, as is less risk, the equally weighted portfolio dominates investing only in Firm 2.
The analysis of equally weighted portfolios is useful for observing the effect of large numbers on portfolio risk, and the elimination of unsystematic risk. We next consider the effects on portfolio risk from relaxing the requirement that portfolio weights be equal. This is covered in the Chapter 4, Markowitz Diversification.
previous topic
next topic
(C) Copyright 1999, OS Financial Trading System