![]() 2.4 SAMPLE STATISTICS: DEFINITIONS
2.4 SAMPLE STATISTICS: DEFINITIONS
Very often in practice investors estimate properties of the underlying probability distribution for a security they are interested in by using a sample of market data constructed from a slice of observed history. Of immediate interest to us is the computation of the mean and variance/covariance matrix from a sample of historic returns. Again for simplicity, we develop this for the discrete random variable case. The same approach is applicable to the continuous case.
Let x be a random variable, and suppose we have N observations of x. The sample mean of x, denoted as M(x), is computed as the simple average of the sample.
![]() .
.
The sample is assumed to be a representative random sample from the true population distribution, and the equal weighting of each observation is equivalent to weighting by probabilities defined as relative frequencies. Recall that in the fundamental analysis approach the analyst is assumed to estimate these probabilities directly and therefore the expected value for the population is computed using the probability weights (see topic 2.3, Population Statistics).
The sample variance of x, is defined as the average sum of squared deviations from the sample mean
![]()
In the estimation of population parameters from sample statistics, we would like our sample statistics to possess "nice properties." One such property is that the expectation of the sample statistic should form an unbiased estimate of the population statistic. That is, its expected estimation error is zero. It turns out that this is not the case for the definition of the sample variance. We explain why in the topic 2.6, Sample Statistics: Unbiasedness. To meet this requirement, we define the sample variance in its unbiased form as:
![]()
Then the sample standard deviation is defined as the square root of the variance:
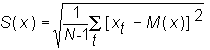
The variance or standard deviation provide a measure of the way the random variable is scattered or dispersed around its sample mean.
Finally, the unbiased sample covariance is denoted as:
![]()
Covariance provides a measure of the degree to which two random variables move together. This covariance figure in its raw form is difficult to interpret because its absolute size depends upon the scale of its unit of measure. To get around this problem covariance is scaled by the product of the two sample standard deviations as follows.
If you have two random variables, say, x and y, then the sample correlation between x and y, is given by:
![]() .
.
In the next topic consistency, we consider the effect of sample size upon estimates of population parameters.
previous topic
next topic
(C) Copyright 1999, OS Financial Trading System