Exactly how risk and return factors influence investor demand is one of the main topics of CAPM Tutor. It is important to realize that the demand for a security cannot be assessed in isolation from other securities in the market. This forms the basis of portfolio diversification, or the theory, "do not put all your eggs into one basket."

We illustrate the principle behind diversification using a historical example. Consider the history of prices for both Chrysler and GM as traded on the New York Stock Exchange (NYSE), shown in Figure 1.2. This time period covered significant events for the automobile industry in general and Chrysler in particular.

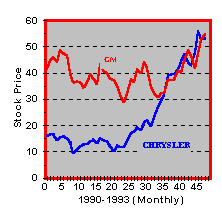
Suppose you purchased one share in both Chrysler and General Motors in January 1990 ($16 for Chrysler, $41 5/8 for GM), held the portfolio for one year, and then sold at $12 5/8 for Chrysler and $36 1/4 for GM. Over this period, you would have received $1.20 per share in dividends from Chrysler and $3.00 from GM. Thus (ignoring the effects of the different times that dividend payments are made), your average return from this equally weighted portfolio of +1 Chrysler and +1 GM is:

Average Return = .5[(12 5/8 + 1.20 - 16)/16] + .5[(36 1/4 + $3.00 - $41 5/8)/$41 5/8]

= .5[-13.6%] +.5[-5.7%]

= -9.65%

If you bought this portfolio at the end of October 1992 and held it for one year, your return would be:

Average Return = .5[(55 7/8+.60-27 1/8)/27 1/8]+.5[(47 5/8+$.80 - $30 3/4)/$30 3/4]

= .5[108.2%]+.5[57.5%]

= 82.85%

If instead you invest solely in Chrysler, your return would be -13.6% and +108.2% over the two time periods. You can see from this that buying GM reduces the variance of your portfolio return. The return is less negative in the first period and less positive in the later one.

You can find information about calculating portfolio returns and variances in Chapter 2, Portfolio Statistics. Chapters 3 and 4, Naive Diversification and Markowitz Diversification, study the effect of forming portfolios on risk and return.

First, however, we will apply two approaches to the problem of forecasting future performance to the Three-Firm Case.

(C) Copyright 1999, OS Financial Trading System