A stock trade is not that different from a simple cash purchase in terms of the nature of what is traded. For example, if you buy a car for cash, the nature of the trade is quite simple : The demander (you) acquires the car, while the supplier receives from you a sum of money.

What happens when you buy a stock? You pay a sum of money (the price of a stock), and you (or, more likely, the brokerage firm) receive a stock certificate. The certificate entitles you to receive the future dividends that are paid by the firm.

In the case of the car, you receive a future flow of services (when you use the car for transportation). In the case of the stock, you receive a future flow of cash (and also some ownership rights in the firm). In either case, you are also free to resell the object.

When you decide to purchase a car, you implicitly place a value today on the flow of services to come to you in the future. Presumably, this value is no less than the price you are willing to pay for the car. When you decide to buy a stock, you similarly place a value on the future cash flows from the stock.

You value future cash flows by discounting them to the present.

The principle of discounting is easy to understand, and arises from the fact that you are not willing to lend $100 today in return for $100 in one year. This embodies the principle of time value of money, and is the basis of the concept of an interest rate.

Simply, all you have to understand is that $100 today is not the same as $100 at some time in the future, but for most of us, is worth more. If it is worth $F > $100 in the future, then the return is the number r such that

F = 100(1 + r).

r is also called the risk-free interest rate.

Here, $F is called the future value of $100 today, and equivalently, $100 is the present value of $F in the future.

Once you recognize that money at different times has different values, it is easy to value a sequence of cash flows. For example, suppose you receive $F in one year and $G in two years. What is this worth today, or, equivalently, what is the present value of this sequence of cash flows? The answer depends on how we discount the future cash flows. If r1 is the interest rate for one period, and r2 is the interest rate for two periods, then the present value is given by

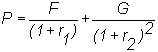
Note that G is discounted by

because the cash flow occurs in two periods.

You may be asking where these interest rates come from. They are determined in a market, just like other prices.

So far, we have looked just at certain cash flows. Uncertainty complicates the picture, because then we have to account not only for the time value of money but also for the risk associated with the cash flows.

To see why uncertainty affects the answer, consider what you would say if you were asked to lend $1,000 today in return for $F in one year. Suppose you reply that $1,100 in one year would be just acceptable to you (implying you need a 10% return to be willing to lend the money). Now, consider your response if you were told that there was a 50% chance that you would not get back anything but also a 50% chance that you could get back $2,200. If you find that now you do not want to lend the money, you would be considered risk-averse. Risk aversion means that you have to be paid a premium (called, appropriately enough, a risk premium) to undertake risk. A risk-neutral person would be willing to lend money at these terms, while a risk-loving person would be willing to accept less than $2,200 to lend the money.

When both time and uncertainty are factors, we have to determine the appropriate interest rates to value cash flows. One answer to this problem is given by the Capital Asset Pricing Model (CAPM). This model, on which CAPM Tutor is based, ends up giving us what are called risk-adjusted discount rates, which can then be used to discount uncertain cash flows. Equivalently the theory gives us risk-adjusted cash flows that can be discounted using the risk free interest rate.

The assumptions underlying the theory are described in the next topic.

(C) Copyright 1999, OS Financial Trading System