Environment

Our goal in this topic is to apply the valuation model for the firm as a whole to determine the market clearing price per share for the Three-Firm Case. The valuation model is as follows:

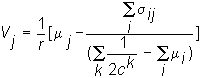
We can compute each of the terms in this valuation model for the Three-Firm Case.

In this example, we assume that investors have two possible quadratic risk-preferences, as we discussed in topic 7.4, Investor Risk Preferences. One has a coefficient of risk-aversion equal to 0.0000525, while the other is less risk-averse, with a coefficient of risk-aversion equal to 0.000025. The quadratic utility function for each investor is:

where

There are three investors of each type, six in all.

The investors are distinguished by both their risk-preferences and their initial holdings of the three companies. The initial holdings of the companies and of cash for each investor are given in Table 7.1.

where the "total preference" equals the summation:

where k = A,B, ...,F.

Observe that half the investors have the 0.0000525 coefficient of risk-aversion and half the 0.000022 coefficient of risk-aversion. In addition, the more risk-averse types (0.0000525) have an initial position that is riskier than the position of the less risk-averse investors; the latter have a risk-free initial endowment. As a result, there are potential gains to trade in this market. We expect the less risk-averse types to be net buyers and the more risk-averse types to be net sellers.

The state dependent cash flows per share are given in Table 7.2:

The aggregate supply of shares of each firm, provided in the bottom row of the endowment table, are 472, 148, and 314 for firms 1,2, and 3 respectively.

From aggregate supplies for this six investor market, the total expected cash flows (aggregate supply times mean expected cash flows value) and the variance covariance matrix (using scientific notation for scaling) for total cash flows can be verified to be:

The summation of the variance/covariance term presented in the last row of Table 7.3 is summing for Firm 1, Firm 2, and Firm 3, respectively, in columns 2, 3, and 4. For example, 5,951,772 is the sum of the covariance terms for Firm 2 with Firm 1, itself and Firm 3.

Finally, let the risk-free rate of return be 12%.

Substituting this information into the valuation equation:

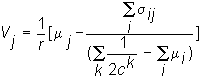
results in the following total value for each firm:

Finally, dividing firm value by the number of shares gives us the stock price for each firm. These are $27.83 for Firm 1, $25.90 for Firm 2, and $25.05 for Firm 3.

The valuation model derived here has important corporate implications, particularly for the capital structure of a firm, i.e. whether the firm issues debt or equity. We discuss this next.

(C) Copyright 1999, OS Financial Trading System