![]() 6.8 SECURITY MARKET LINE
6.8 SECURITY MARKET LINE
So far, we have concentrated on deriving the efficient frontier, which is the set of portfolios that provide the least risk given any target return. Next, we start characterizing individual security returns. The result we are after is that the expected return on any individual security can
always be written as a linear combination of two portfolios on the minimum-variance frontier. This is a central part of the capital asset pricing model, to be interpreted further when we study market equilibrium. We first obtain this combination when one portfolio consists only of the risk-free asset. The general case, when all assets are risky, is covered in the topic Zero-Beta Portfolios.We have identified the capital market line as well its tangency with the minimum-variance frontier. This tangency point defines a particular portfolio of risky securities, which we call M. This lets us start to consider the implications this has for individual security returns. In particular, we can write
![]()
which shows that the expected return on security i is a linear combination of the risk-free return and the return on portfolio M. You will see that this relationship is a consequence of efficient set mathematics. The coefficient
b measures the risk of security i, and is related to the covariance of security i with the tangency portfolio, M. Thus, the expected return will equal the risk-free asset plus a risk premium, where the risk premium depends on the riskiness of the security. The equation that describes the expected return for security i, is called the security market line (SML).The risk/return relationship for security i is a purely mathematical relationship, derived in topic 6.9, titled Derivation of the SML. In Chapter 7, Capital Market Equilibrium, you will see that in equilibrium, M can be computed from market prices and is the portfolio of all risky assets in the market. You can recall that, the line passing through the risk-free asset's risk/return point and portfolio M's risk/return point, is the capital market line. The slope of this line is the market price of risk.
In the SML equation expected returns are linear and the coefficent beta is:
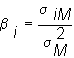
The SML is sometimes called the Capital Asset Pricing Model (CAPM) equation. It tells you the relationships that must be satisfied among the security's return, the security's beta and the return from portfolio M. Note that this is a general relationship that embraces not only individual securities but portfolios as well. This is because i can be any security or portfolio.
Let us interpret what the security market line says. In words, the expected return of a risky security i equals the risk-free rate of return plus some additional return weighted by this term "beta." The additional return is the excess of the return that portfolio M provides over the risk-free rate of return weighted by beta. That is, if beta equals one then this target return exactly equals the target return of M.
Recall, that i can be any security or portfolio of securities. Therefore, the SML relationship implies that the beta of portfolio M itself equals one. Similarly, from this relationship the beta of the risk-free security is zero. As a result, beta is a very convenient measure of the risk of a security in a capital market.
You may ask: Why is beta a measure of risk? To address this question let us take an equivalent look at the security market line by writing the slope of the capital market line as
l',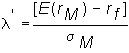 ,
,
The SML can now be written as:
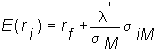
In this form, the SML is a linear function of the covariance of an asset with the market portfolio. This relationship makes a lot of sense if we recall that the risk of an individual security is its contribution to the total risk of a portfolio to which it belongs. Thus for any risky security i the covariance between i's return and M's return provides a measure of its contribution to the total risk of M.
The general derivation of the SML is provided in topic 6.9, titled Derivation of the SML, and then to make the security market line a little more concrete, we construct this line in topic 6.10, Three-Firm Case: Derivation of the SML.
previous topic
next topic
(C) Copyright 1999, OS Financial Trading System