Naive diversification refers to the formation of equally weighted portfolios. Here we want to examine the impact of naive diversification on portfolio risk. Recall, that portfolio risk is defined as the standard deviation of portfolio returns, which we cover in Chapter 2 (see topic 2.9, Portfolio Statistics).

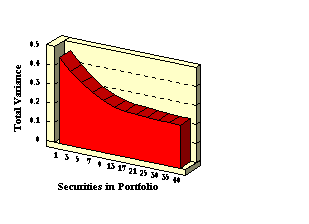
A major advantage of quantifying risk is that you can then identify both analytical and empirical properties of risk. Many empirical studies have examined the impact of portfolio size on portfolio risk. A common finding (e.g., see, Evans and Archer (1968)) is that the diversification benefits, provided from randomly forming equally weighted portfolios of different sizes, become insignificant beyond 15 to 20 securities. This result is graphed in Figure 3.1. It means that a small low-transaction cost portfolio can be almost as effective as a very large naively formed portfolio.

To understand why this is so, let us consider the expressions for the sample variance and standard deviation of portfolio returns. The sample variance is defined as:

The covariance term (cov) is the sample variance when i equals j, and the sample covariance when i is not equal to j. Note that there are n variance terms and n(n - 1) covariance terms, and we can write the sample variance as:

If variances are all finite (i.e., bounded above by some number "var"), and covariances are all finite (i.e., bounded above by some number "covar"), then we can rewrite this equation as:

The first term on the right hand side of this equation reduces to (var/n) and the second term [(n-1)covar]/n. Since both "var" and "covar" are finite numbers, as n grows large, the first term approaches zero and second term approaches covar. Therefore, the variance terms (i.e., the firm-specific risk) become negligible, and can be called diversifiable risk. Since the covariance terms remain, this source of risk is referred to as non-diversifiable.

These concepts are applied to the Three-Firm Case.

(C) Copyright 1999, OS Financial Trading System